Info
This work was done during my internship at Blueshift with Guy Gur-Ari and Behnam Neyshabur.
Abstract
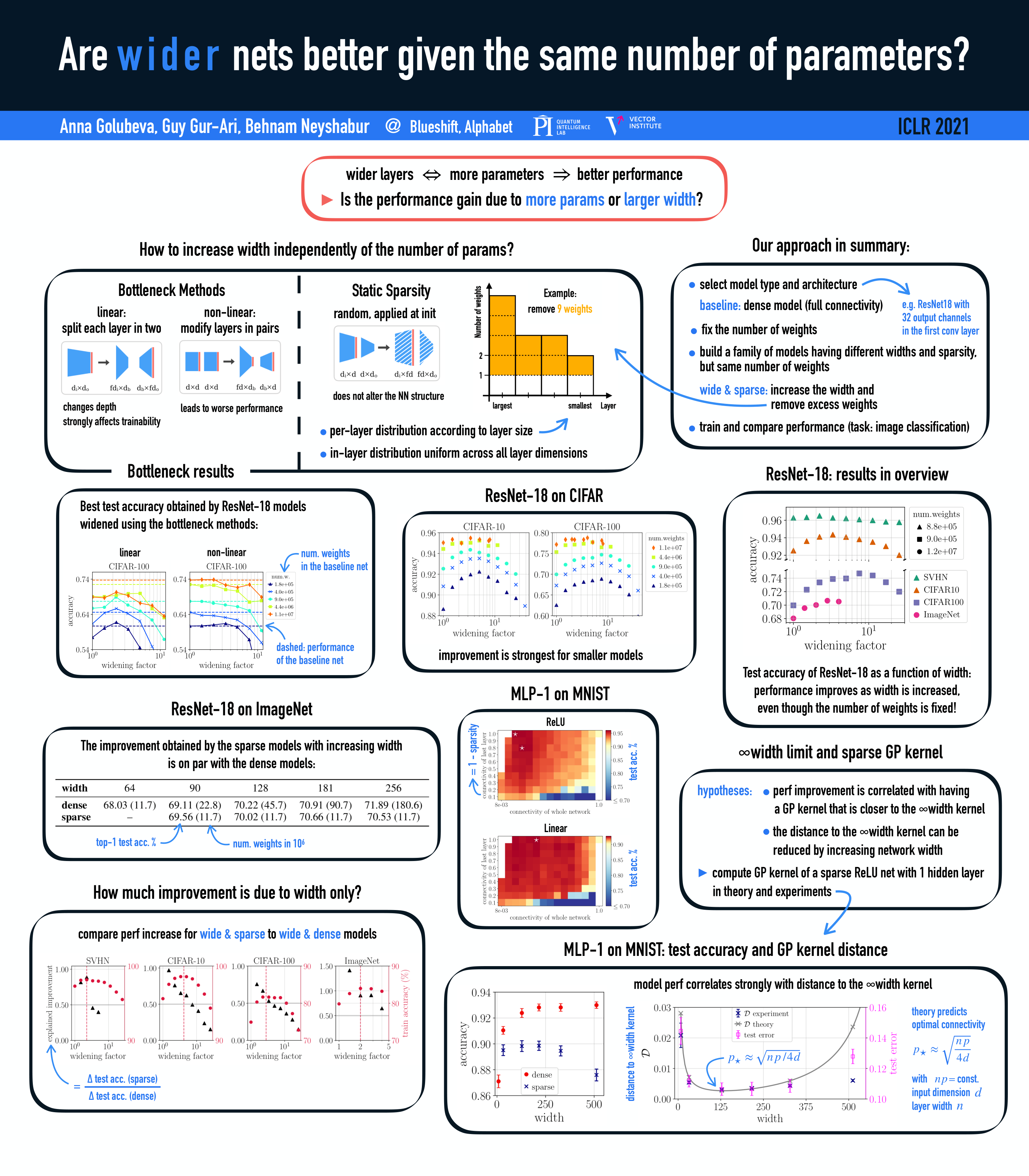
Empirical studies demonstrate that the performance of neural networks improves with increasing number of parameters. In most of these studies, the number of parameters is increased by increasing the network width. This begs the question: Is the observed improvement due to the larger number of parameters, or is it due to the larger width itself? We compare different ways of increasing model width while keeping the number of parameters constant. We show that for models initialized with a random, static sparsity pattern in the weight tensors, network width is the determining factor for good performance, while the number of weights is secondary, as long as the model achieves high training accuarcy. As a step towards understanding this effect, we analyze these models in the framework of Gaussian Process kernels. We find that the distance between the sparse finite-width model kernel and the infinite-width kernel at initialization is indicative of model performance.
Talk
I presented this work at ICLR 2021 as a poster (see below), at the Sparse Neural Networks 2021 workshop, and in several invited talks, some of which were recorded. For a short version, check out the ICLR webpage, and for a long version, see this talk I gave at Physics ∩ ML:
Poster
Here is the poster presented at ICLR 2021: